对散列表数据结构的简单分析记录
一、什么是Hash表
Hash函数:地址index=H(key)
说白了,hash函数就是根据key计算出应该存储地址的位置,而哈希表是基于哈希函数建立的一种查找表。
二、哈希函数的构造方法
根据前人经验,统计出如下几种常用hash函数的构造方法:
直接定址法
直接定址法(Direct Addressing)是一种特殊的哈希函数,它将关键字直接映射到哈希表的索引上。这种方法适用于关键字集合的大小与哈希表的大小相等的情况。下面我将提供一个更直观的例子来说明直接定址法。
假设一个图书馆有一本特殊的书籍,这本书记录了该图书馆所有书籍的索引信息。每本书都有一个唯一的ISBN号,我们可以用这个ISBN号作为关键字来构建哈希表。
- 哈希表大小:假设哈希表有100个槽位(索引从0到99)。
- 哈希函数:我们可以定义一个简单的哈希函数,将ISBN号的最后两位数字直接用作索引。哈希函数可以表示为 H(ISBN) = (ISBN % 100),其中ISBN是书籍的ISBN号。
假设有以下几本书的ISBN号:
- 978-0-306-40615-7
- 978-1-4028-9462-6
- 978-0-387-34586-9
计算哈希值:
- 对于第一本书,H(978-0-306-40615-7) = (978030640615 % 100) = 15
- 对于第二本书,H(978-1-4028-9462-6) = (978140289462 % 100) = 62
- 对于第三本书,H(978-0-387-34586-9) = (978038734586 % 100) = 86
哈希表建立
| index | ISBN | 书名 |
|---|---|---|
| 15 | 978-0-306-40615-7 | “Book A” |
| 62 | 978-1-4028-9462-6 | “Book B” |
| 86 | 978-0-387-34586-9 | “Book C” |
在这个例子中,我们可以看到直接定址法如何将ISBN号映射到哈希表的索引上。这种方法的优点是简单且直接,但缺点是哈希表的大小必须与关键字集合的大小相匹配,这在实际应用中可能不太灵活。
数学分析法
假设关键字集合中的每个关键字key都是由s位数字组成 $(k_1, k_2 , … , k_n)$, 分析key中的全体数据,并从中提取分布均匀的若干位或他们的组合构成全体
我们知道身份证号是有规律的,现在我们要存储一个班级学生的身份证号码,假设这个班级的学生都出生在同一个地区,同一年,那么他们的身份证的前面数位都是相同的,那么我们可以截取后面不同的几位存储,假设有5位不同,那么就用这五位代表地址。 H(key)=key%100000 此种方法通常用于数字位数较长的情况,必须数字存在一定规律,其必须知道数字的分布情况,比如上面的例子,我们事先知道这个班级的学生出生在同一年,同一个地区。
平方取中法
如果关键字的每一位都有某些数字重复出现频率很高的现象,可以先求关键字的平方值,通过平方扩大差异,而后取中间数位作为最终存储地址。
比如key=1234 1234^2=1522756 取227作hash地址
比如key=4321 4321^2=18671041 取671作hash地址
这种方法适合事先不知道数据并且数据长度较小的情况
$H(key)= floor((key^2 / (10^k)) mod \space m)$ 其中 k 是一个常数,用于控制取多少位。
折叠法
当关键字位数较多时,可以将其分成几部分,然后对每部分进行哈希,最后将这些哈希值合并。
例如,可以将关键字分成高位和低位两部分,分别计算哈希值,然后合并。
除留余数法
除留余数法用的较多 H(key)=key MOD p (p<=m m为表长) 很明显,如何选取p是个关键问题。
比如我们存储3 6 9,那么p就不能取3
因为 3 MOD 3 == 6 MOD 3 == 9 MOD 3
p应为不大于m的质数或是不含20以下的质因子的合数,这样可以减少地址的重复(冲突)
比如key = 7,39,18,24,33,21时取表长m为9 p为7 那么存储如下
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| key | 7 | 21(冲突后移) | 24 | 39 | 18(冲突后移) | 33(冲突后移) |
随机法
在某些情况下,可以使用随机数来构造哈希函数,以增加哈希值的随机性和均匀性。 例如,可以生成一个随机的哈希表,其中每个槽位都有一个随机的哈希函数。
H(key) =Random(key) 取关键字的随机函数值为它的散列地址
hash函数设计的考虑因素
- 计算散列地址所需要的时间(即hash函数本身不要太复杂)
- 关键字的长度
- 表长
- 关键字分布是否均匀,是否有规律可循
- 设计的hash函数在满足以上条件的情况下尽量减少冲突
三、哈希冲突
公共溢出区法
建立一个特殊存储空间,专门存放冲突的数据。此种方法适用于数据和冲突较少的情况。
再散列法
准备若干个hash函数,如果使用第一个hash函数发生了冲突,就使用第二个hash函数,第二个也冲突,使用第三个……
开放寻址法
首先有一个H(key)的哈希函数
如果$H(key_1)=H(key_i)$
那么$key_i$存储位置 $H_i = (H(key)+d_i) MOD \space m$,m为表长。
$d_i$ 有三种取法
1) 线性探测再散列 $d_i = c * i$
2) 平方探测再散列 $d_i = 1^2,(-1)^2,2^2,(-2)^2$
3) 随机探测再散列(双探测再散列)$d_i$是一组伪随机数列
注意,增量$d_i$应该具有以下特点(完备性):产生的Hi(地址)均不相同,且所产生的s(m-1)个Hi能覆盖hash表中的所有地址
- 平方探测时表长m必须为4j+3的质数(平方探测表长有限制)
- 随机探测时m和di没有公因子(随机探测di有限制)
链地址法
产生hash冲突后在存储数据后面加一个指针,指向后面冲突的数据:
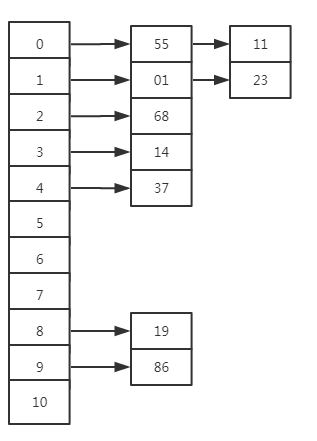
四、hash表的查找
查找过程和造表过程一致,假设采用开放定址法处理冲突,则查找过程为:
对于给定的key,计算hash地址index = H(key)
如果数组arr【index】的值为空 则查找不成功
如果数组arr【index】== key 则查找成功
否则 使用冲突解决方法求下一个地址,直到arr【index】== key或者 arr【index】==null
hash表的查找效率
决定hash表查找的ASL(Average Search Length)因素: 1) 选用的hash函数 2) 选用的处理冲突的方法 3) hash表的饱和度,装载因子 α=n/m(n表示实际装载数据长度 m为表长)
一般情况,假设hash函数是均匀的,则在讨论ASL时可以不考虑它的因素 hash表的ASL是处理冲突方法和装载因子的函数 前人已经证明,查找成功时如下结果:

可以看到无论哪个函数,装载因子越大,平均查找长度越大,那么装载因子α越小越好?也不是,就像100的表长只存一个数据,α是小了,但是空间利用率不高啊,这里就是时间空间的取舍问题了。通常情况下,认为α=0.75是时间空间综合利用效率最高的情况。
上面的这个表可是特别有用的。假设我现在有10个数据,想使用链地址法解决冲突,并要求平均查找长度<2 那么有1+α/2 <2 α<2 即 n/m<2 (n=10) m>10/2 m>5 即采用链地址法,使得平均查找长度< 2 那么m>5
hash表的ASL是基于装载因子的函数,也就是说,当数据n增加时,我可以通过增加表长m,以维持装载因子不变,确保ASL不变。
那么hash表的构造应该是这样的:

五、hash表的删除
链地址法:每个哈希槽位对应一个链表,删除元素只影响该链表,不影响其他元素的查找。
开放定址法:所有元素直接存储在哈希表的槽位中。删除元素时,不能简单地将槽位留空,因为这会打断探测序列,导致无法找到后续插入的元素。正确的做法是使用一个特殊值或标记(如-1)来表示该槽位的元素已被删除,从而保持探测序列的完整性。
参考
- 数据结构(严蔚敏)
- https://blog.csdn.net/u011109881/article/details/80379505